Both stocks and bonds are cores pieces of an investment portfolio. However, understanding how bonds work isn’t easy. It often remains a mystery for many investors. In this entry, we’ll review how bonds work, how they’re valued, and why the ‘yield to maturity’ is so important. In a second part, we’ll explore the relationship between interest rates and bond prices and the risks of investing in bonds.
The basics of bonds
What are bonds?
In simple terms, a bond is a loan that you make to others [1]. Others are typically either governments or companies. Unlike you, when these institutions need money, they often don’t go to a bank and ask for a loan. Instead, they issue bonds. And investors buy these bonds. By buying bonds, investors are effectively giving a loan to the issuer.
Why are bonds so important?
Bond are a nice tool to have in every investor’s belt because of three reasons:
- Predictability of returns: the cash flow of bonds is deterministic. This means that you know in advance exactly how much money you’ll receive when. Compared to stocks, there’s less uncertainty. We know from investing 101 that low uncertainty is equal to low volatility. And that low volatility investments are relatively safe investments
- Suitability for short investment horizons: mostly because of their lower volatility, bonds are well suited for the short term. They’re a great way to park cash that you know you’ll need in the next 1-5 years
- Diversification: historically, bonds and stocks have been less than perfectly correlated. In plain terms, this means that their prices don’t always move together. When stocks appreciate, bonds might appreciate, keep their value, or depreciate. And vice-versa. This translates into a great diversification potential. If you hold both stocks and bonds, your portfolio will be less bumpy than if you only hold stocks
Bonds vs stocks – which one is better?
Neither. They’re different. With stocks nothing is promised, but the potential gain is unlimited. With bonds everything is determined in advance, but you won’t get more than that.
In general, the predictability of returns makes bonds a safe choice compared to stocks. But you pay a price for it. Long term returns of bonds have historically been about half of stocks [2]. However, historically paints nowadays too good a picture for bonds. Bond yields have plummeted over the last couple of decades.
How much you invest in bonds vs stocks depends on your risk tolerance and your investment horizon. In general, the higher your risk tolerance and investment horizon, the more you should invest in stocks. And the less in bonds. And vice-versa. For example, if you can park your money for 30 years and can psychologically deal with volatility, you should stick mostly to stocks. Conversely, if you’re planning to buy a house in 4 years, a bond-heavy allocation is a better idea. Stocks would be way too risky. There’s no guarantee of positive returns in the stock market over just 4 years.
How do bonds work?
Time to get into the nitty-gritties of bonds. To understand how bonds work, you first have to understand what defines a bond. Two of the most important characteristics of a bond are its principal and its maturity.
The principal (also called face value or par value) is the amount of money that is paid back to the investor sometime in the future. The maturity is the period of time after which the principal is repaid.
Let’s look at an easy example. Imagine the price of a bond today is $960. It has a maturity of 2 years. Its face value is $1,000. That means that you pay $960 today and you get $1,000 back in 2 years.
Alright, maturity and face value are clear. But there’s more to it. Bonds often pay coupons as well. A coupon is a periodic interest payment made by a bond. It’s often expressed as a percentage of the principal. Coupons are typically paid either once or twice per year.
Let’s look at another example. Say we have a bond with maturing in 4 years with a face value of $1,000 and a 3% yearly coupon. You can buy the bond for $980. How would your cash flows look like?
| Today | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|
| -980 | 30 | 30 | 30 | 1,030 |
You’d get $30 in years 1, 2, and 3. In year 4, you’d get another $30 plus the $1,000 principal.
How do you value a bond?
You now understand how bonds work. But there’s something we’ve been neglecting. In our last example, we took for granted that the bond had a price of $980. Where does this come from? Who sets this price? Is it the issuer? It’s not. The price of a bond is determined by interest rates.
To understand how interest rates affect the price of a bond, you need to understand how discounting works. Discounting means determining the value today of a payment received in the future. If you don’t know how discounting works, check this entry before you continue reading.
Valuing a bond means determining its price. To value a bond, you simply add up all discounted cash flows it generates. This results in a fair price. In our example, the price of $980 assumed a constant interest rate per year of 3.5%. Check the table to see how we valued the bond. Remember that the discounted cash flows are the cash flows divided by the discounting factor.
| Date | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|
| Cash flow | 30 | 30 | 30 | 1,030 |
| Interest rate | 3.5% | 3.5% | 3.5% | 3.5% |
| Discounting factor | (1 + 0.035)^1 | (1 + 0.035)^2 | (1 + 0.035)^3 | (1 + 0.035)^4 |
| Discounted cash flow | ~29 | ~28 | ~27 | ~897 |
If you add up all discounted cash flows (29 + 28 + 27 + 897) you get to ~980. This is the value of the bond given current interest rates.
You normally don’t have to calculate the prices of bonds yourself. Much like stocks, you can assume that their market value already reflects the correct pricing logic. Still, as a future bond investor, you have to understand how bonds are valued. At least conceptually. It’s a key aspect of how bonds work.
Bonds and the yield to maturity
Congrats! You’ve graduated from bonds 101. You now know what’s the principal, the maturity, the coupon and how to value a bond.
There’s more you need to know, though. The yield to maturity (YTM) is a key metric of a bond. Read this section carefully. The YTM is the most useful measure to understand the expected return of a bond. You must understand YTMs if you ever want to invest in bonds.
What is the yield to maturity
In analytical terms, the YTM is the single interest rate that explains the value of a bond. This might confuse you. Wasn’t it 3.5% for our last example? Yes, it was! In the example above, the YTM was 3.5%.
Unfortunately, calculating the YTM is not always that easy. Why? Because, in our example, we assumed that the interest rate was constant and equal to 3.5% for all years. This is not a realistic assumption. In general, the longer the time horizon, the higher interest rates. The relationship between maturity and interest rates is called a yield curve. And typically looks like this (source):
Let’s look at another example. We’ll value a bond maturing in 3 years with a face value of $1,000 and a 2% yearly coupon. We’ll use the yield curve above. Make sure that interest rates in the table check out with the chart:
| Date | Year 1 | Year 2 | Year 3 |
|---|---|---|---|
| Cash flow | 20 | 20 | 1,020 |
| Interest rate | 0.41% | 1.01% | 1.57% |
| Discounting factor | (1 + 0.0041)^1 | (1 + 0.0101)^2 | (1 + 0.0157)^3 |
| Discounted cash flow | ~20 | ~20 | ~973 |
We know that the value of a bond is the sum of the discounted cash flows. In this case, that sum is $1,013.
What’s the yield to maturity of this bond? Remember that the YTM is the single interest rate that, applied to all years, results in the the same total discounted cash flow of $1,013. In other words, you have to solve for YTM in the table below so that CF1 + CF2 + CF3 = $1,013:
| Date | Year 1 | Year 2 | Year 3 |
|---|---|---|---|
| Cash flow | 20 | 20 | 1,020 |
| Interest rate | 0.41% | 1.01% | 1.57% |
| Discounting factor | (1 + YTM)^1 | (1 + YTM)^2 | (1 + YTM)^3 |
| Discounted cash flow | CF1 | CF2 | CF3 |
This is a bit trickier to solve. You need Excel or a financial calculator. The answer is YTM = 1.55%. You can try to plug it in and see what you come up with. The YTM is very close to the interest rate of year 3 because the cash flow in year 3 is much bigger than the others.
What does the yield to maturity tell you?
Enough with the math. You won’t have to calculate the YTM yourself anyways. It’s important to know how the YTM is calculated, but it’s even more important to know what it means.
The YTM is the annualized return that an investor receives if (s)he holds the bond until it matures*. Read this sentence twice. And think about it implies. When you’re buying bonds, the YTM tells you what your yearly return will be until the bond matures.
The coupon is not a good measure for your returns. Whether the price of a bond is below or above its face value is not a good measure for your returns. Only the yield to maturity matters.
*Some fine print here: this assumes that you reinvest all coupons received at a rate equal to the YTM itself. This is difficult to prove. But easy to understand intuitively. Just draw a parallel with stocks. For stocks, you get the index total return if you reinvest all dividends into the index. For bonds, you get the YTM if you reinvest all coupons at a yield equal to the YTM
So that means….
In our example before, the price of the bond was $1,013. The YTM is 1.55%. The YTM is the annualized return you’d get if you hold the bond to maturity. So each year you get 1.55%. Your total return after three years would be (1 + 1.55%)^3 – 1. That’s about 4.7%. Or around $48 on top of your $1,013 investment.
Interest rates vs bond yields – don’t get confused!
A common pain point for new investors is to differentiate between yields – including bond yields and yield to maturity – and interest rates. For our practical purposes, they’re the same thing. You just saw in our example how much the interest rate in year 3 influenced the YTM of the bond. They were pretty much the same thing. If interests rate goes up, YTM goes up. If interest rates goes down, YTM goes down. Just keep in mind that interest rates ~= yields ~= yield to maturity.
If you know a bond’s YTM, you know its price, and vice-versa
Determining the YTM of a bond is exactly the same thing as determining its price. Why? Because you can assume that the maturity, face value and coupon rate of a bond are known and fixed. The only thing you’re missing to value the bond and get its price is the YTM. If I tell you one, you can give me the other.
Do I have to calculate the YTM before I trade a bond?
No, you don’t. You’ll find it calculated already. It changes all the time depending on the supply and demand for bonds. In a way, the YTM is determined by the market. This might sound strange at first. But it’s easy to understand if you draw a parallel with stocks. When you look at a share of Tesla you don’t have to calculate its price, do you? Whatever the price is, it’s determined by the market. Same goes for bonds prices. Bond prices are determined by the market. And because knowing the YTM means knowing the price of a bond, the YTM must be determined by the market too.
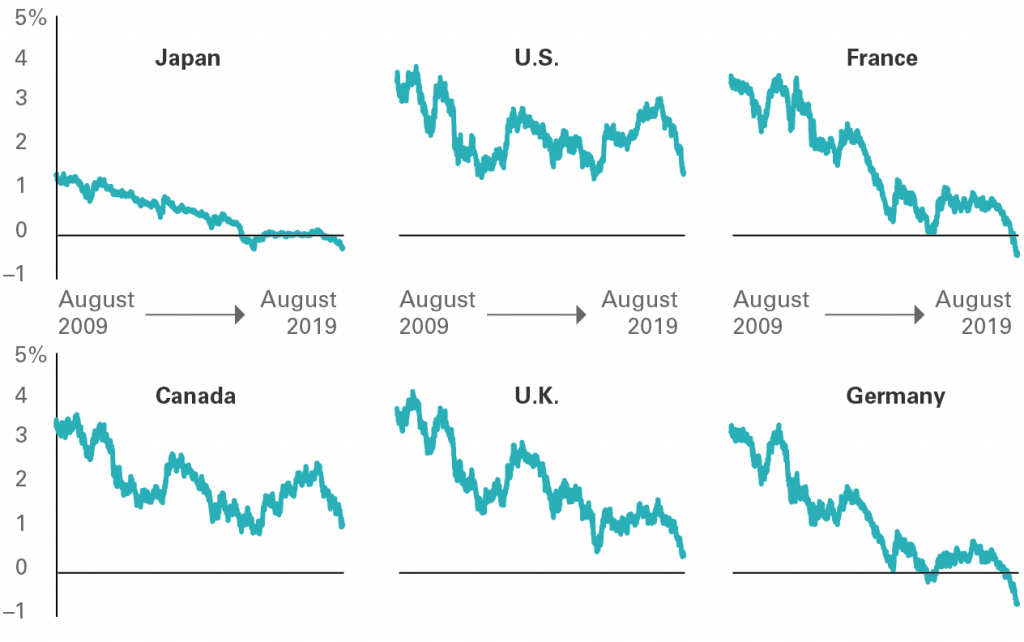
YTMs over the last decade
Before, we said that bond yields have plummeted over the last couple of decades. These yields are YTMs. Now you’re in a position to understand what this implies. Look at the image below. See why bonds are nowadays in a tough spot?
Clarification on the yield curve
We saw that the yield curve is most often upward sloping. This translates into higher YTMs for bonds with longer maturity. This might naturally draw you towards long term bonds. They have more attractive returns, right? Why not invest only in long term bonds? Wouldn’t this be sensible? Not always.
For starters, beyond ~15 years stocks are a relatively safe bet. And they will very likely return more than bonds. There’s little point in holding to maturity a 30-year bond.
Long term bonds are terrible investments
Warren Buffet (watch here)
Besides, bonds with longer maturities have a higher interest rate risk. We’ll cover interest rate risks in detail in the second part of the entry.
The bottom line is: don’t be seduced by the higher YTMs of long term bonds. They have other drawbacks. For long investment horizons (say 15+ years), consider stocks.
Closing
In case you didn’t get it all…
By now you’ve experienced first-hand that bonds are a tricky business. If this is the first time you’re exposed to bonds, it’s highly likely that you didn’t get it all. Don’t despair. It’s normal. You might have to re-read this entry or check out additional material for the concepts to sink in.
What we’ve learned
Completing this entry means you’ve been exposed at least once to the basics of bonds. Well done! We’ve seen why bonds are important. What’s the meaning of coupon, face value and maturity. How to value a bond given a yield curve. And why knowing the YTM is the same as knowing the price of a bond. Most importantly, we saw that the YTM is the best measure of expected returns. Not the coupon, the face value, or the price.
Ready for more?
You’ve come a long way. But there’s more that you need to know before investing in bonds. You still have to learn important concepts such as interest rate risk, credit risk, duration and OTC trading. You’ll find out about those in the second part of how bonds work. For now, make sure you consolidate what you’ve learned so far. It will all come back. Ready when you are.
Last updated on May 6, 2020