The time value of money is a critical concept in finance. It affects the value of every financial asset. From stocks & bonds to mortgages. Yet the meaning of ‘time value of money’ often remains cryptic. What exactly is the time value of money? And how does it affect you?
The intuition behind time value of money
The basic premise of time value of money is that money received today is worth more that money received in the future. This is intuitive to most people. If I gave you the option to get for free $10k today of $10k in a year from now, you’d likely rather have the money today. The key question is: why? Well, you probably understand that having the money today gives you more options than having it in the future. There’s value in having the money early. In essence, this is the time value of money [1].
Time value of money in the context of investing
Let’s dig a bit further. Imagine a scenario in which you can invest money and get a guaranteed return of 10% per year. With zero risks. In this scenario, would you rather have $10k today or $11k in a year from now? You likely still prefer the $10k today. After all, you can transform $10k into $11k a year later yourself. You just have to invest the money. But you’d probably agree that the two options are kind of fair, right? They’re properly balanced.

Now imagine that some offers you to have $10k today or $10.5k in a year from now. What would you say? This is an easy one. You’ll always get the $10k today. I mean, if you don’t need the money now, you can invest and have $11k in a year, right? With the $10.5k you feel like you’re not being compensated enough for the year you wait. The time value of money is higher than what you’re being offered.
A final deal. Say that the two options are $10k today or $12k in a year from now. This one is trickier, isn’t it? $12k in a year is more than you could get by investing. At least with zero risks. If you don’t need the money right now, you might actually prefer to wait.
If you followed along, then you understand the time value of money from an investment perspective. Because you forego potential returns by not having money now, having the money now is better than later.
Time value of money in the real world
Let’s ditch our imaginary scenario. How does the time value of money play out in the real world?
In the real world, there’s no such thing as a zero risk investment. But some options come darn close. Treasury Bills (T-Bills) are considered an almost risk-free investment [2]. T-Bills are short term bonds issued by the US government. There are equivalents for most countries. These short term bonds are fully backed up by governments and their money printing presses. So it’s extremely unlikely they won’t be repaid.
This family of super-safe short term government bonds doesn’t yield anything close to 10% a year, though. For US T-Bills, it’s more like 0.2% at the time of writing. But the concept is the same. You can transform money into more money in an almost risk-free way in the real world. You just need time. Your money has time value because it’s worth more earlier than later.
From time value of money to discounting
The process how humans mathematically calculate the time value of money is called discounting. Discounting means determining the value today of a payment to be received in the future. The value today is often called the present value (PV). And the value in the future is called the future value (FV).
Linking present value and future value
Bringing present and future value together is easy. We’ve implicitly done it already in our imaginary 10% risk-free return scenario. Let’s do it explicitly now.
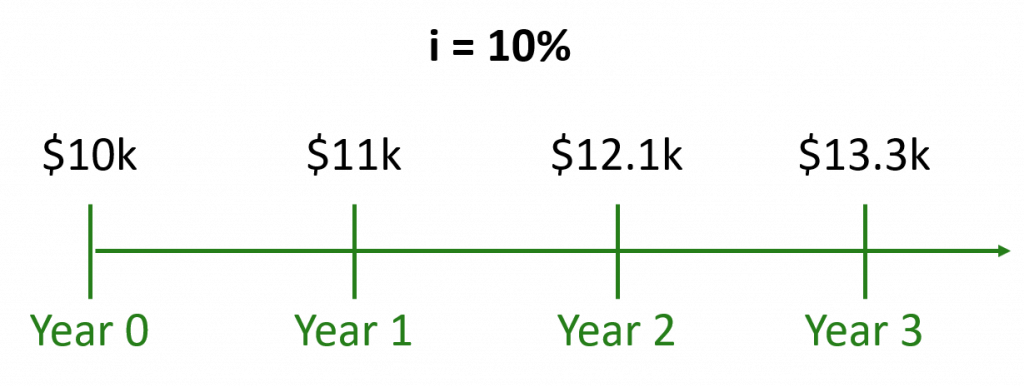
What’s the future value, one year from today, of $10k if we assume a 10% risk-free rate? $11k. How do you get to it?
Future value = $10k * (1 + 10%) = $11k
What about in 2 years from now? The first year would be the same. But in the second year, you could invest the full $11k you have after year 1. In the end you’d end up with:
Future value = $10k * (1 + 10%) * (1 + 10%) = $12.1k
It keeps going:
The general formula is:
Future value (FV) = Present value (PV) * (1 + interest rate)^periods
Stop and look at this equation for a moment. It’s quite powerful. The future value of an asset is linked to its present value. And the only linking variable is the interest rate.
Discounting
Discounting is the opposite of calculating future values. If you understand the formula above, then you know how to discount already. You just have to solve for PV:
Present value (PV) = Future value (FV) / (1 + interest rate)^periods
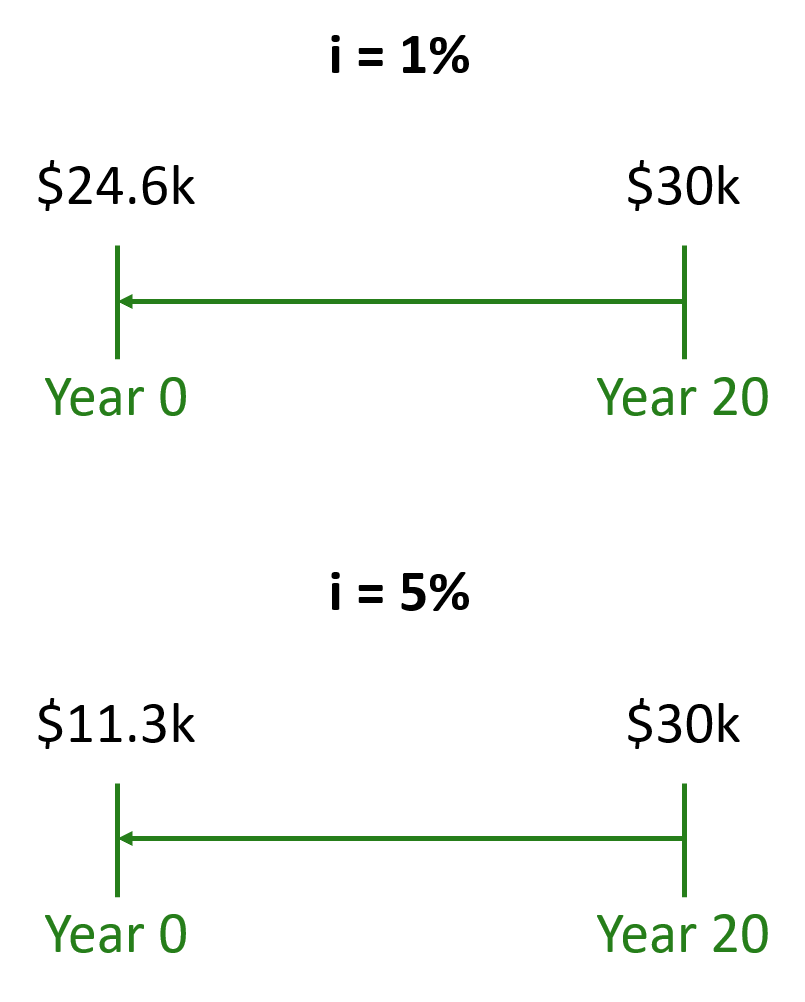
Assume a risk-free interest rate of 1%. What’s the PV of $30k received 20 years from now? It’s $24.6k. What if the interest rate was 5%? Then the PV would be just $11.3k.
Why discounting is so important
As an investor, discounting is important because it’s used to value most financial assets. Valuing an asset means estimating its price today. For example, if we value a bond, we are determining its price today.
How exactly does it happen? You bring all future cash flows to today. In other words, you discount all future cash flows and them up together. What are these cash flows? They depend on the asset class:
- Bonds: cash flows are the coupon payments and the final repayment of principal. Check this entry for an example of how you value a bond by discounting its cash flows
- Real estate (e.g. a house): cash flows might be the monthly rental income
- Stocks: cash flows are the dividends you receive
You often don’t have to value financial assets yourself. But it’s basic financial literacy to know how it works. At least conceptually.
The discount rate
We use the discount rate to bring future values back to the present. So far we’ve seen we can do this using interest rates. But that’s just one of several alternatives. The following are typical parameters often used as a discount rate:
- Interest rates: these are almost always yields from safe bonds. You use safe bonds because you don’t want to factor in additional financial risk. Interest rates make sense in the context of investing or financial markets. You might also consider inflation by discounting using real rates instead of nominal rates
Real interest rate = nominal interest rate – expected inflation - Required rate of return: the required rate of return (RRR) is the minimum return an investor is willing to accept [3]. Setting the discount rate equal to your RRR makes it easy to evaluate investing options. For example, if your RRR is 6%, any investment that brings you future values lower than that will result in a negative present value
- Opportunity cost of capital: a typical approach for companies is to use opportunity cost as a discount rate. Opportunity cost is the ‘loss’ of not using the money for other purposes. In the context of a company, other purposes could be other projects. If you know that you can make 3% a year by investing in a different project, it makes sense to discount using that rate
Don’t worry if you don’t understand everything in the list above. Getting the concepts of time value of money and discounting is more important than the specific discount rate you use.
Clarification on time
We’re using years in all our examples because it’s the easiest to conceptualize. You can also discount or calculate future values using a different time basis. And even convert from one time basis to another. For that, you need the adjust the discount rate. For example, you can convert a yearly discount rate to a monthly or daily one. Whatever you do, the core ideas behind the time value of money and discounting remain the same.
The compounding effect
The compounding effect is the additional returns you get by reinvesting previous gains. It’s tightly connected to everything we’ve seen until now.
A simple example
Let’s go back to our scenario with a risk-free return of 10%. This time we’ll go a bit further into the future:
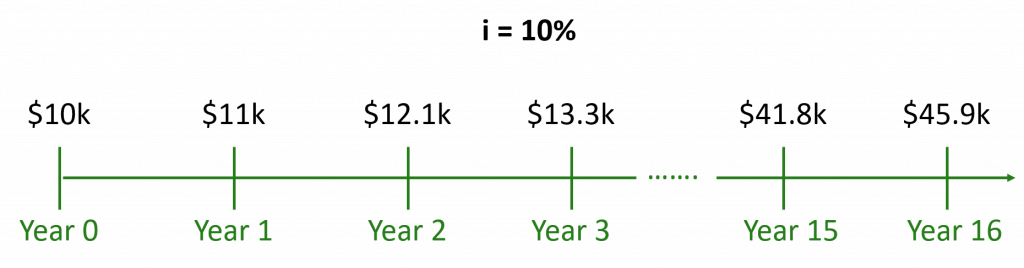
We’re assuming we reinvest all our gains. Thanks to that, we can see the compounding effect in action. How to see it? Notice how your yearly returns get bigger and bigger as time goes by. You made:
- $1.0k from year 0 to 1
- $1.1k from year 1 to 2
- $1.2k from year 2 to 3
- $4.1k from year 15 to 16. This is more than the first three years combined!
Compounding is often thought of as going from present value to future value. But it works exactly the same way when we discount.
The compounding effect amplifies with time
As time goes by, the compounding effect becomes and more important. This is one of the reasons why you want to invest long term. In the chart below, we compare a compounded growth that assumes reinvestment of all previous gains with a constant growth that doesn’t. Notice how the curves start to diverge more and more as time goes by. The the gap after 20 years is more than 2x. The longer the time horizon, the higher the influence of the compounding effect.
The compounding effect in reality
Where can we see the compounding effect in real life? Anytime you invest. Think about buying stocks. Say you buy an index fund for $100. After a year it appreciates to $105. If you don’t sell anything, you now have $105 invested. You’re reinvesting your gains. If the stock appreciates by 5% again, you’ll be benefiting from the compounding effect already.
More generally speaking, returns from stocks come from two sources. Price returns and dividend returns. Price returns are the example we just saw. Dividend returns are regular payouts companies make. Price returns are by definition gains automatically reinvested. Dividends aren’t. You can choose if you want to reinvest dividends or not. If you do, you’ll amplify the compounding effect. Which is desirable.
What you’ve learned
Money and time are linked. It’s not the same to have money now than to have money in the future. By reading this entry, you’ve learned:
- What’s the time value of money
- How to link present values and future values
- What’s discounting
- Why discounting is important
- What are different types of discount rates
- What’s the compounding effect and how it can benefit you
Last updated on May 23, 2020